Zeit für eine neue Erddruck-Lehre

Ausführlich werden vorgestellt die derzeitige Lehre in den PDF’s der Uni München www.lrz-muenchen.de und die Grundlagen der neuen Erddruck-Theorie im Web unter www.erddruck.de.

Beim Aufbau der neuen Theorie war es erforderlich einige Begriffe neu zu bestimmen, wie Gleit-, Neigungs- und Scherebene, wobei die Gleitebene (alt) der Reibungs- und Neigungsebene (neu) entspricht. Die Scherebene wurde als Begriff übernommen, jedoch mit anderer Lage und Winkel im Erdkeil. Versuchsanordnungen mit unterschiedlichen Bodenarten ließen erkennen, dass Böden sich nur auf der Neigungsebene (neu) bewegen und der Tangens des Neigungswinkels ß der Reibungszahl µ entspricht (µ = tan ß → ß).

Die natürliche (neue) Schwerebene mit dem Scherwinkel s stellt sich ein als Böschungsebene, wenn Boden aus einer Grabenwand ohne externe Druckausübung abgleitet und beim Abgleiten nicht auflockert (tan s = tan ß /2 → s). Derzeit wird der Scherwinkel δ über Probekörper im Labor erkundet, wobei axialer oder triaxialer Druck auf den Probekörper ausgeübt wird. Der Druck macht die Scherwinkel ungleich (s ≠ δ).

Für wenige Bodenarten können Kenngrößen derzeit aus Tabellen getrennt nach bindigen und nicht bindigen Böden entnommen werden, wobei die Namen der Bodenarten ortbezogen unterschiedliche Bedeutungen haben können.
Um zukünftig den Bodenarten unverwechselbare Eigenschaften zuordnen zu können, setzt die neue Theorie auf Raum- und Gewichtsteile getrockneter Böden, denen dann theoretisch das entzogene oder erwartete Wasser wieder zugegeben wird. Die Trennung von Feststoff- und Porenvolumen sowie Wasser erlaubt es dem natürlichen Bodenverhalten gezielter nachgehen zu können.

Bei der Berechnung der Raumteile wird davon ausgegangen, dass alle Bodenarten Erosionsprodukte von Felsgesteinen magmatischen, metamorphen oder sedimentären Ursprungs sind. Während bei der fortschreitenden Verwitterung die Masse des Feststoffanteils gleich bleibt, vergrößert sich der Porenanteil des neuen Bodens. Reduziert man die erweiterte Masse wieder auf einen Kubikmeter, so verändert sich lediglich das Verhältnis zwischen Feststoff- und Porenvolumen (Vp = Vf + Vl = 1,00 m³).

Ordnet man als Dichten dem harten Felsgestein (Basalt) ρ₉₀ = ptg = 3,0 t/m³ und Wasser ρ_w = pwg = 1,0 t/m³ zu, so lässt sich unter Vernachlässigung des Gewichtes des Porengases das Trockengewicht jeder Bodenart über das spezifische Feststoffvolumen multipliziert mit der Felsdichte errechnen. Fügt man zur Trockendichte das Porenwasser hinzu, so können auch die Eigenschaften feuchter oder nasser Böden exakt ermittelt werden. Des Weiteren zeigt das Verhältnis von Feststoff- zu Porenvolumen eines getrockneten Bodens den Tangens des Neigungswinkel ß an, und damit auch die Reibungszahl (µ = Vf / Vl = tan ß)

Belegt man den obersten Punkt einer Ordinatenachse mit dem harten Basaltgestein (Dichte ptg₉₀ = 3,0 t/m³, ß = 90°) und den Nullpunkt mit dem Urstaub (ptg₁ = 0,03 t/m³, ß = 0,6°) und erstellt über dieser Achse mit der Höhe h einen Halbkreis, so stellen die am Nullpunkt unter dem Neigungswinkel ß angetragenen Linien bis zum Kreisbogen die Hangabtriebsebenen der unterschiedlichen Bodenarten dar, die Linie von den Hangabtriebsebenen bis zum obersten Pol der Achse die Normalkraftebenen und die waagerechten Abstände vom Kreisbogen bis zur Ordinatenachse die Ebenen des Erddrucks (H-Kräfte) dar.
Zur Ermittlung des Neigungswinkels ßn feuchter oder nasser Böden ist aus dem Wasser ein fiktives Feststoffvolumen zu bilden (Vf’ = V_w /ρ₉₀) und in die nachstehende Formel einzufügen: tan ßn = Vf / (Vl + V_w /ρ₉₀) → ßn.

Der natürliche Scherwinkel feuchter oder nasser Böden stellt sich ein unter tan sn = tan ßn /2 → sn.

Da alle Bodenarten, vom angewitterten Fels bis hin zum Urstaub über den natürlichen Reibungswinkel Spannungen erzeugen, können sie nicht als ‚feste Körper’ im Sinne der Physik betrachtet werden, d.h. eine Kraftverteilung nach dem Gesetz der ‚geneigten Ebene’ ist gegeben.

Bei beiden Verfahren wird in der Regel die Erddruckkraft / Gewichtskraft errechnet über die Lastfläche (A-C-B) mal Berechnungstiefe a = 1,00 m multipliziert mit der Bodendichte und Fallbeschleunigung. Da die Gewichtskraft auf einer geneigten Ebene (C-B) aufsetzt, ist sie immer aktiv, auch wenn sich der Boden hinter der Wand nicht bewegen kann.

Die neue Theorie kennt daher weder einen „aktiven“, einen „erhöhter aktiven“ und einen „passiven“ Erddruck“, welche nach derzeitiger Lehre von der Bewegung der belasteten Fläche abhängig sein sollen.

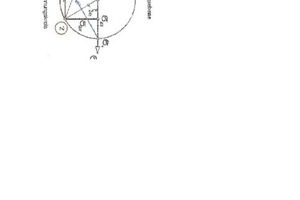
Während die neue Theorie die Gewichtskraft über das physikalische Gesetz der ‚geneigten Ebene’ direkt in horizontale und vertikale Kraftkomponenten umwandelt, bedient sich die Lehre der Kraftverteilung über den ‚Mohrschen Spannungskreis’, d.h. über die Scherebene und setzt diese in der Höhe h/3 an. Winklig zur Scherebene baut sie die Neigungsebene (alt) auf und nutzt die Lage dieser Ebene um die Gewichtskraft auf die Normal- und Hangabtriebskraft zu verteilen. Sie geht hierbei davon aus, dass es eine ‚Wandreibung’ gibt, die von der Rauigkeit der erdberührten Fläche abhängig sein soll. Die neue Theorie erkennt hier weder eine Wandreibung noch die Bildung eines Wandreibungswinkels δ; denn ohne Bodenbewegung kann keine Reibung an der Wandfläche entstehen.

Die Darstellung des Spannungskreises, hier um 90° gedreht, ist aus der PDF-Datei Seite l5 des Zentrum Geotechnik entnommen, s. www.lrz-muenchen.de
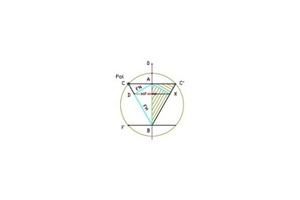
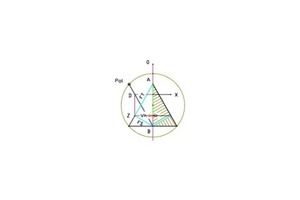
Bei dieser Darstellung fällt auf, dass der Scherwinkel δ = 2α betragen soll, wobei doch der natürliche Scherwinkel s dem Ansatz tan 2α entspricht. Berücksichtig man den Winkel 2α, so wird der Punkt 0 aus dem Spannungskreis herauskatapultiert, s. Abb. 7 u. 8.

Unter der Voraussetzung, dass Boden hinter einer lotrechten Wand auf der Neigungsebene (neu) abgleiten kann, bildet sich die natürliche Schwerebene s aus und nimmt im Bereich der ursprünglichen Wand die Höhe h/2 an und nicht die Höhe h/3 nach derzeitiger Lehre. Versuche mit Bodenarten lassen annehmen, dass der Erdmantel aus „Erdblöcken“ besteht, die sich in „stehende“ und „liegende“ Erdkeile unterteilen, wobei die Spitze des stehenden Keils nach unten und die Spitze des liegenden nach oben zeigt. Fügt man beide Keilformen zusammen, entsteht ein Erdblock. Vervollständigt man die Keilformen im Erdblock durch Spiegelung, so lässt sich erkennen, dass für eine Kraftverteilung nach dem Mohrschen Spannungskreis in der Physik kein Raum ist, wie die Abb. 7 u. 8. zeigen.

Derzeitig wird – soweit vorhanden – die Kohäsion als Kraft bei der Erddruckermittlung berücksichtigt. Die neue Theorie stellt die Kohäsion in den Zusammenhang mit dem Porenwasser. Ihre Kraft kann damit den Erddruck weder erhöhen noch reduzieren; sie kann Bodenbewegungen aber beeinflussen, d.h. beschleunigen oder verzögern.

Einerseits die Vielzahl der gravierenden Mängel in den Berechnungsvorgaben der derzeitigen Lehre, wie die Kraftverteilung über die Scherebene und den Ansatz des Erddrucks für alle Bodenarten in der Höhe h/3, und andererseits die eindeutige Bestimmung der Bodeneigenschaften über die Raum- und Gewichtsteile von Böden, die Abkehr der Kraftverteilung von dem Schwerpunkt aus und die Nutzung des physikalischen Gesetzes der „geneigten Ebene zur Kraftermittlung lassen erkennen, dass die derzeitige Lehre ihren Anspruch verloren hat, weiterhin Grundlage von Regelwerken oder Normen zu sein. Es ist Zeit für eine neue ErddruckLehre!n